들어가며
벌써 알고리즘 2주차가 지났다. 그래프, 특히 DFS를 다루면서 러닝커브가 급격히 상승한 느낌 탓에 좌절을 맞보기도 했지만 LeetCode 기준 Easy ~ Medium 난이도의 문제는 풀 수 있는 수준으로 개념이 잡힌듯 하다. 이번 회고록에서는 그래프와 그래프 탐색 기법인 DFS, BFS에 대해서 간략하게 정리하고, 추후 더 보완해야 할 부분에 대해서 정리하도록 하겠다.
저번주까지만 하더라도 내가 푼 문제를 바로 정리해서 블로그에 업로드 하곤 했는데, 이번주는 문서화하는 과정이 정말 어렵게 느껴졌다. 그 이유 중 하나로는 재귀함수의 추상적인 특징 때문인 것 같다. 문제 하나를 설명하기 위해서는 여러 장의 그림이 필요한데, 짧은 시간에 여러 개념을 접한 탓에 쫒기듯이 문제를 풀다보니 스스로 정리할 시간이 부족했던 것 같다(완벽하게 개념을 숙지하지는 못했다는 의미이기도 하다).
그래프
자료구조는 크게 선형구조, 비선형구조로 구분된다. 선형구조는 자료를 저장하고 꺼내는 것에 초점이 맞춰져 있는 반면, 비선형구조는 표현에 초점이 맞춰져있다고 한다. 그래프는 연결되어 있는 정점과 정점간의 관계를 표현할 수 있는 비선형구조의 자료구조이다. 그래프의 연결 관계를 가진 각 데이터를 노드(Node)라고 하는데 이를 정점(Vertex)이라고도 한다. 그리고, 노드 간의 관계를 나타낸 선을 간선(Edge)이라고 하며, 간선으로 직접 연결된 노드를 인접 노드(Adjacent Node)라고 한다.
선형구조의 연결 리스트를 비선형구조로 나타낸 것이 그래프라고 생각한다.
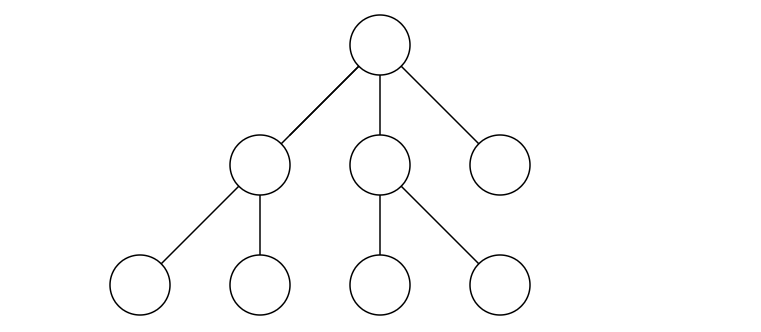
여기서 다루는 대부분의 그래프는 2차원인데, 이를 탐색해야 하는 경우 X축을 먼저 탐색할 것인지, Y축을 먼저 탐색할 것인지 고민을 해보아야 한다. 이때, X축을 먼저 탐색하는 경우를 BFS(너비 우선 탐색), Y축을 먼저 탐색하는 경우를 DFS(깊이 우선 탐색)라고 할 수 있다.
DFS
DFS(Depth First Search)는 깊이 우선 탐색을 의미하며, 현재 노드의 Y축 방향으로 연결된 가장 깊숙한 노드까지 우선 탐색하는 방식을 말한다.
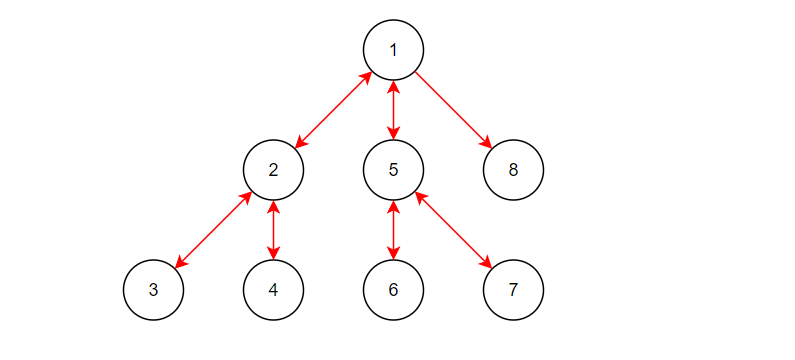
DFS를 구현하는 방법으로는 크게 반복(Iterative)과 재귀(Recursive)가 있다. 먼저, 반복은 우리에게 익순한 for문 이나 while문을 통해 그래프를 탐색하는 방식이며, 특정 노드를 방문한 적이 있는지 확인하기 위해 Stack, Queue 등의 자료구조를 사용한다. 반면, 재귀는 조건에 맞는 탐색을 완료할 때까지 함수를 반복적으로 호출하는 방식이다. 재귀는 메모리 스택(후입선출)에 함수를 차곡차곡 쌓아놓고, 가장 최근에 호출된 함수를 먼저 처리하는 방식으로 연산을 처리한다.
BFS
BFS(Breadth First Search)는 너비 우선 탐색을 의미하며, 현재 노드가 존재하는 층의 모든 노드를 탐색한 후 다음 층으로 이동하는 방식을 말한다.

DFS는 현재 노드의 하위 노드를 우선으로 탐색하기 때문에 주로 재귀함수로 구현하는 반면, BFS는 현재 노드와 가까운 노드를 먼저 탐색하기 때문에 주로 Queue를 사용해서 구현한다.
예제
그렇다면 어떻게 DFS와 BFS를 구현할 수 있는지 LeetCode 200번 문제를 통해 알아보도록 하자. 문제의 내용을 정리해보면 다음과 같다.
- M × N으로 구성된 2차원 그래프가 배열로 주어진다.
- 이 그래프는 섬을 의미하는데, 1은 땅, 0은 물을 의미한다.
- 주어진 그래프를 통해 섬의 개수를 파악해야 한다.
grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]위의 입력값을 그림으로 나타내면 다음과 같다.
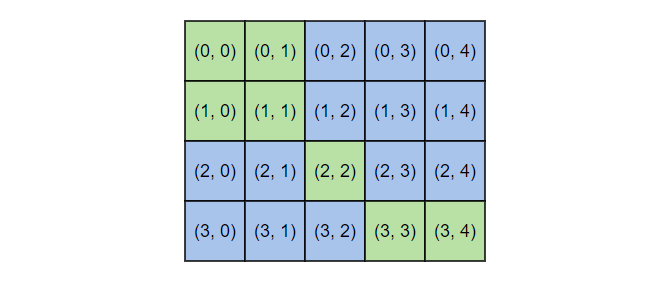
문제에서 말하는 섬의 개수는 곧 1의 연속성을 의미한다. 즉, X축과 Y축 방향으로 1이 연속적으로 연결되어 있는지 파악하면 되는데, X축을 먼저 탐색하고자 하는 경우 BFS, Y축을 먼저 탐색하고자 하는 경우 DFS를 사용하면 된다.

공통사항
DFS 또는 BFS로 접근하기 전에 공통적인 부분 먼저 해결하고 넘어가도록 하자. 문제에서 주어진 배열에서 인접한 노드를 찾기 위해서는 현재 노드를 기점으로 위, 아래, 왼쪽, 오른쪽 노드를 전부 둘러보아야 할 것이다. 이를 위해서 임시 좌표를 다음과 같이 정해놓았다.
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]그리고, 현재 주어진 그래프의 크기를 알기 위해서 행과 열의 길이가 몇인지도 알아야 할 필요가 있다.
rows = len(grid)
cols = len(grid[0])마지막으로 섬의 개수를 최종적으로 반환해야 하므로 다음과 같이 변수를 초기화해주어야 한다.
cnt = 0
# ... (로직) ...
return cntDFS 풀이
먼저, DFS로 접근하는 경우를 살펴보자. DFS는 그래프의 아래 방향을 먼저 탐색하는 방식이므로 열 -> 행 순으로 반복하도록 하였다.
사실 이 문제를 완벽히 이해하고 나면, x축을 먼저 탐색하든 y축을 먼저 탐색하든 크게 상관없다는 것을 알게 된다. 즉, 그래프를 90도 회전시키면 x축과 y축이 바뀌기 때문에 DFS로
행 -> 열순으로 반복해도 상관없다.
for col in range(cols):
for row in range(rows):
pass우리는 섬의 개수 즉, 1의 연속성만 파악하면 된다. 따라서, 현재 좌표의 값이 1이 아닌 경우(즉, 1의 연속성이 깨진 경우) 다음 행으로 이동시켜주는 조건을 먼저 작성하자. 이와 같은 조건을 반복문 초기에 해준다면 불필요한 탐색(상하좌우)을 하지 않게되므로 수행 시간을 조금 더 단축시킬 수 있다.
for col in range(cols):
for row in range(rows):
if grid[row][col] != "1":
continue그리고, 현재 노드(grid[row][col])가 1인 경우(즉, 1이 연속되는 경우)에는 섬의 시작이라고 할 수 있기 때문에 섬의 개수를 1 증가시켜준다.
for col in range(cols):
for row in range(rows):
if grid[row][col] != "1":
continue
cnt += 1이제 DFS를 Iterative로 구현할 것인지, Recursive로 구현할 것인지에 따라 코드가 달라지나, 동작 방식은 완전히 똑같다고 할 수 있다. 먼저, Iterative로 구현한 코드는 다음과 같다.
class Solution1:
def numIslands(self, grid: List[List[str]]) -> int:
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
rows = len(grid)
cols = len(grid[0])
cnt = 0
for col in range(cols):
for row in range(rows):
if grid[row][col] != "1":
continue
cnt += 1
stack = [(row, col)]
while stack:
x, y = stack.pop()
grid[x][y] = "0"
for xx, yy in zip(dx, dy):
nx = x + xx
ny = y + yy
x_limit = nx < 0 or nx >= rows
y_limit = ny < 0 or ny >= cols
if x_limit or y_limit:
continue
if grid[nx][ny] != "1":
continue
stack.append((nx, ny))
return cnt코드를 보면 Stack을 사용한 것을 알 수 있다. 이 로직을 간단하게 설명하면 다음과 같다.
실제 Stack이 아닌 리스트를 사용해서 Stack의 작동 방식(LIFO)을 나타냈다.
- 1을 발견한 경우, 현재 좌표를 스택에 넣는다.
- 상하좌우의 모든 값을 확인한다.
- 상하좌우를 살피는 도중에 좌표를 벗어나면 건너뛴다.
- 상하좌우에 해당하는 좌표가 유효한 좌표인 경우 좌표를 스택에 추가한다.
- 여기까지의 과정을 반복하고 다음 행으로 이동한다.
이를 Recursive로 나타내면 다음과 같다.
class Solution2:
def numIslands(self, grid: List[List[str]]) -> int:
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
rows = len(grid)
cols = len(grid[0])
cnt = 0
def recursive(rx, cy):
x_limit = rx < 0 or rx >= rows
y_limit = cy < 0 or cy >= cols
if x_limit or y_limit:
return
if grid[rx][cy] != "1":
return
grid[rx][cy] = "0"
for xx, yy in zip(dx, dy):
recursive(rx + xx, cy + yy)
return
for col in range(cols):
for row in range(rows):
if grid[row][col] != "1":
continue
cnt += 1
recursive(row, col)
return cntIterative에서는 while문을 통해 상하좌우를 살펴보았다면, Recursive에서는 재귀함수로 상하좌우를 살펴본다는 점만 다를 뿐 모든 로직은 똑같다는 것을 알 수 있다. 즉, 같은 로직을 다르게 표현한 것이라고 할 수 있겠다.
과제톡 발표에서 실무에서는 재귀함수를 거의 사용하지 않는다는 말을 들었다. 그 이유는 메모리 스택에 쌓이는 방식의 재귀호출 때문이다. 만약, 재귀호출 횟수가 메모리의 스택영역을 벗어나게 되면
Stack Over Flow오류가 발생하게 된다. 즉, 정상적인 로직으로 코드를 작성하여도 하드웨어에서 문제가 발생할 수 있으므로 안정성이 떨어진다는 특징이 있다.
BFS 풀이
이번에는 BFS로 해결한 코드를 살펴보자. 아래 코드를 보면 행 -> 열 순으로 반복을 진행했다는 점 외에는 전부 같은 코드라는 것을 알 수 있다. 책에서는 BFS를 주로 Queue로 구현한다는 내용을 본 적이 있으나, 이는 상황에 따라 다를 것으로 생각된다.
class Solution3:
def numIslands(self, grid: List[List[str]]) -> int:
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
rows = len(grid)
cols = len(grid[0])
cnt = 0
for row in range(rows):
for col in range(cols):
if grid[row][col] != '1':
continue
cnt += 1
stack = [(row, col)]
while stack:
x, y = stack.pop()
for xx, yy in zip(dx, dy):
nx = x + xx
ny = y + yy
x_limit = nx < 0 or nx >= rows
y_limit = ny < 0 or ny >= cols
if x_limit or y_limit:
continue
if grid[nx][ny] != "1":
continue
grid[nx][ny] = '0'
stack.append((nx, ny))
return cnt위의 코드에서 Stack을 대신해서 Queue로 나타내면 다음과 같다.
실제 Queue가 아닌 리스트를 사용해서 Queue의 작동 방식(FIFO)을 나타냈다.
class Solution4:
def numIslands(self, grid: List[List[str]]) -> int:
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
rows = len(grid)
cols = len(grid[0])
cnt = 0
for row in range(rows):
for col in range(cols):
if grid[row][col] != '1':
continue
cnt += 1
q = [(row, col)]
while q:
x, y = q[0]
q = q[1:]
for xx, yy in zip(dx, dy):
nx = x + xx
ny = y + yy
x_limit = nx < 0 or nx >= rows
y_limit = ny < 0 or ny >= cols
if x_limit or y_limit:
continue
if grid[nx][ny] != "1":
continue
grid[nx][ny] = '0'
q.append((nx, ny))
return cnt마치며
약 2주 후 알고리즘 주차가 끝나면 지금 알고 있는 이 내용은 머릿속에서 흐릿해지겠지만, 이 글은 계속 남아있을 것이게 때문에 가장 기초적인 개념을 정리해보았다.
그래프와 DFS, BFS를 정확히 이해하였는가?라는 질문에 '그렇다'라고 명확하게 말하지는 못하겠다. 이번 알고리즘 주차로 하여금 전체적인 큰 밑그림을 한 번 그려본 듯한 느낌이다. 내게 부족한 점을 파악했으니, 항해를 졸업한 이후에도 자료구조와 알고리즘 공부는 계속 이어나갈 예정이다.
혼자 알고리즘 공부할 때에는 그래프 개념이 나오면 프로그래밍의 흥미를 잃지 않기 위해 배열, 문자열 문제만 찾아다니곤 했는데, 항해99라는 시스템 안에서 어떻게는 해결하기 위해 공부를 해야된다는 점에서 항해99라는 시스템의 장점이 돋보이는 것 같다(물론, 장점만 있다는 뜻은 아니다).
'Development > 회고록' 카테고리의 다른 글
| 백엔드 개발자, 첫 스타트업 퇴사일기 (43) | 2023.12.05 |
|---|---|
| 항해99 Chapter #2 - 2주차(자료구조 - 연결 리스트, 스택과 큐, 해시 테이블) 회고록 (0) | 2022.03.20 |
| 항해99 Chapter #1 - 1조 S.A(Starting Assignment) (0) | 2022.03.07 |
| 스파르타코딩클럽 내일배움단 완주 후 회고록 (2) | 2022.02.19 |