문제
문제의 내용을 간단히 요약하자면, 입력받은 번호에 해당하는 알파벳을 순서대로 조합한 문자열을 반환하는 것이다. 예를 들어, 아래와 같이 '234'를 입력받았을 때, 조합한 문자열의 길이는 입력받은 문자열의 길이와 동일하게 3이어야 하며, 각각 ['abc'] + ['def'] + ['ghi'] 순서대로 조합된 모든 문자열을 찾아야 한다.
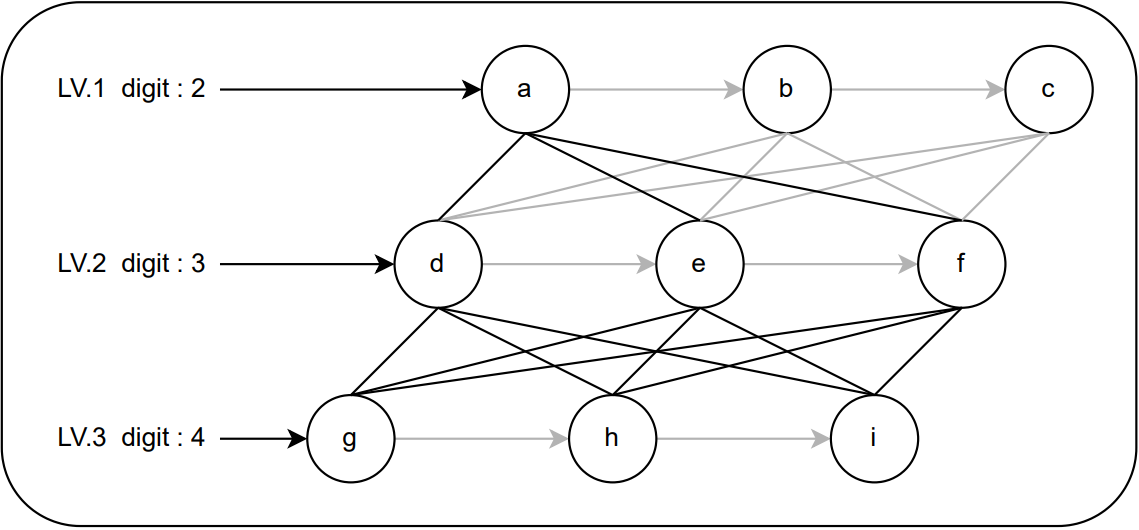
input : ['234']
output: ['adg', 'adh', 'adi', 'aeg', 'aeh', 'aei', 'afg', 'afh', 'afi', 'bdg', 'bdh', 'bdi', 'beg', 'beh', 'bei', 'bfg', 'bfh', 'bfi', 'cdg', 'cdh', 'cdi', 'ceg', 'ceh', 'cei', 'cfg', 'cfh', 'cfi']이는 깊이 우선 탐색(DFS) 문제에 해당하며, 번호(다이얼)에 해당하는 문자열을 해시맵으로 만들어 놓은 후 두 가지 방식(소스코드)으로 문제를 해결할 수 있다.
dials = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz"
}iterative 방식
이 방식은 반복문으로 해결한 방식으로 다음과 같은 로직으로 접근해보았다.
반복문을 통해 다이얼의 번호에 맞는 문자열을 해시맵에서 꺼내온다.
chars = [dials[digit] for digit in digits]첫 번째 다이얼에 해당하는 문자열을 리스트로 초기화한다.
res = list(chars[0])첫 번째 다이얼에 해당하는 문자열을 제외한 나머지 문자열을 반복하며 현재 리스트에 저장된 문자열과 다음 문자열의 모든 문자를 조합한다(삼중 반복). 그리고 현재 리스트를 새롭게 조합된 문자열 리스트로 바꿔준다.
for char in chars[1:]:
res = [f"{r}{c}" for c in char for r in res]위의 코드에서 res가 바뀌는 과정을 print로 출력해보면 다음과 같다.
(init) ['a', 'b', 'c']
(loop #1) ['ad', 'bd', 'cd', 'ae', 'be', 'ce', 'af', 'bf', 'cf']
(loop #2) ['adg', 'bdg', 'cdg', 'aeg', 'beg', 'ceg', 'afg', 'bfg', 'cfg',
'adh', 'bdh', 'cdh', 'aeh', 'beh', 'ceh', 'afh', 'bfh', 'cfh',
'adi', 'bdi', 'cdi', 'aei', 'bei', 'cei', 'afi', 'bfi', 'cfi']LeetCode에 제출하여 총 8번 실행한 결과 평균 속도는 44ms(42ms ~ 46ms), 메모리는 13.9MB ~ 14.0MB인 것을 알 수 있었다. 그리고 주어진 입력값 N개에 대해서 삼중 반복문을 수행하므로 시간 복잡도는 O(N3)이라고 생각한다.
recursive 방식
이 방식은 재귀함수를 호출하는 방식이며, 책의 내용(338쪽 12장 그래프 참고)을 바탕으로 코드를 작성하였기 때문에 실행 결과만을 비교해보았다.
def recursive(index, path) -> None:
if len(path) == len(digits):
return res.append(path)
for i in range(index, len(digits)):
for c in dials[digits[i]]:
recursive(i+1, f'{path}{c}')
res = []
recursive(0, "")
return res마찬가지로 res에 문자열이 추가되는 과정을 print로 출력한 후 첫 번째 노드(a, b, c)를 기준으로 구분하면 다음과 같다.
(init) []
(path: "a~") ['adg', 'adh', 'adi', 'aeg', 'aeh', 'aei', 'afg', 'afh', 'afi']
(path: "b~") ['bdg', 'bdh', 'bdi', 'beg', 'beh', 'bei', 'bfg', 'bfh', 'bfi']
(path: "c~") ['cdg', 'cdh', 'cdi', 'ceg', 'ceh', 'cei', 'cfg', 'cfh', 'cfi']LeetCode에 제출하여 8번 실행한 결과 평균 속도는 52ms(44ms ~ 64ms), 메모리는 13.9MB ~ 14.0MB인 것을 알 수 있었다. 그리고 DFS 하나당 이중 반복을 수행하므로 시간 복잡도는 O(N2)이며, M개의 정점에 대해 DFS로 모두 탐색해야 하므로 시간 복잡도는 O(N2 * M)이라고 생각한다.
전체 코드
from typing import List
dials = {"2": "abc", "3": "def", "4": "ghi", "5": "jkl",
"6": "mno", "7": "pqrs", "8": "tuv", "9": "wxyz"}
# iterative
class Solution1:
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return []
if len(digits) == 1:
return list(dials[digits])
chars = [dials[digit] for digit in digits]
res = list(chars[0])
for char in chars[1:]:
res = [f"{r}{c}" for c in char for r in res]
return res
# recursive
class Solution2:
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return []
def recursive(index, path) -> None:
if len(path) == len(digits):
print(res)
return res.append(path)
for i in range(index, len(digits)):
for c in dials[digits[i]]:
recursive(i+1, f'{path}{c}')
res = []
recursive(0, "")
return res마치며
'오늘은 DFS를 배웠으니 DFS로만 문제에 접근해보아야지'라는 생각이 무의식중에 자리잡았던 것 같다. 그런데, 책에서 나온 코드를 직접 작성하고, print로 로그를 찍어보면서 '어쩌면 반복문으로 구현할 수도 있겠다'라는 생각이 들었고, 조합을 직접 손으로 작성한 후에는 비교적 간단하게 구현할 수 있었다. 재귀함수를 거의 써본 경험이 없어서 그런지 이해는 되는데 머릿속에서 그려지지가 않는다. DFS 문제가 나올 때마다 iterative와 recursive 방식을 모두 구현해보면서 이 둘을 자유자재로 변형할 수 있도록 많은 연습이 필요할 것 같다.
'Algorithm > LeetCode' 카테고리의 다른 글
| LeetCode #561 - Array Partition I(배열 파티션 1) 풀이 (0) | 2022.03.17 |
|---|---|
| LeetCode #015 - 3Sum(세 수의 합) 풀이 (0) | 2022.03.16 |
| LeetCode #409 - Longest Palindrome(가장 긴 팰린드롬) 풀이 (0) | 2022.03.16 |
| LeetCode #622 - Design Circular Queue(원형 큐 디자인) 풀이 (0) | 2022.03.16 |
| LeetCode #232 - Implement Queue using Stacks(스택을 이용한 큐 구현) 풀이 (0) | 2022.03.16 |